6ES7 215-1BG40-0XB0型号介绍






6ES7 215-1BG40-0XB0型号介绍
直流在数控中曾得到广泛的应用,它具有良好的调速和转矩特性,但是它的结构复杂、制造成本高、体积大,而且电机的电刷容易磨损,换向器会产生火花,使直流伺服电机的容量和使用场合受到限制。交流伺服电机没有电刷和换向器等结构上的缺点;并且随着新型功率开关器件、专用、计算机技术和控制算法等的发展,促进了交流驱动电路的发展,使得交流伺服驱动的调速特性更能适应进给伺服系统的要求。现代数控机床都倾向采用交流伺服驱动,交流伺服驱动大有取代直流伺服驱动之势。
1.交流伺服电机的结构
交流电机有交流感应电机和交流同步电机之分。交流感应电机结构简单、容量大、价格低,一般用作主运动的驱动电机。
永磁同步交流伺服电机用作进给运动的驱动电机,其结构示意如图1所示。电机由定子、转子和检测元件组成。定子由冲片叠成,其外形呈多边形,没有机座,这样有利于散热。在定子齿槽内嵌入某一极对数的三相绕组。转子也由冲片叠成,并在其中装有磁铁,组成的极对数与定子的极对数相同。磁铁有:铝镍钴合金、铁淦氧合金和钕铁硼合金即稀土永磁合金等,以稀土永磁合金的性能好。检测元件一般都用脉冲编码器,也可用旋转变压器加测速发电机,用以检测电机的转角位置、位移和旋转速度,以便提供永磁交流同步电机转子的位置信息、位置反馈量和速度反馈量。

图1 永磁同步交流伺服电机结构示意图
2.交流伺服电机的变频调速
交流的转速n,与交流频率f,电机极对数p以及转速滑差率s之间的关系为
![]() (1)
(1)
对于异步电机s≠0,对于同步电机则s=0。由式(1)可知,改变电源的频率f,电机的转速n与f成正比例变化。电机定子绕组的反电势为
e=4.44fwkwφ
如果略去定子的阻抗压降,则定子相电压
u≈e=4.44fwkwφ
上式说明,kw为常数,若相电压u不变,则随着频率f的升高,气隙磁通φ将减小。又从转矩公式
![]()
可以看出,φ值减小,电机转子的感应电流i2也相应减小,势必导致电机的允许输出转矩m下降。另外,若相电压u不变,随着f的减小,气隙磁通φ将增加,这会使磁路饱和,激磁电流上升导致铁耗剧增,功率因数下降。因此改变频率f进行调速时,需要同时改变定子的相电压u,以维持φ值接近不变,从而使m也接近不变。可见交流伺服电机变频调速的关键问题是要获得调频调压的交流电源。
调频调压电源有很多种。通常采用交流-直流-交流的变换电路来实现,这种电路的主要组成部分是三相电流逆变器。图2所示是目前应用广泛的电压型功率晶体管(gtr)三相逆变器主回路原理图。由交流-直流变换的整流电路获得恒定的直流电压ud,功率晶体管开关元件t1、t4,t3、t6,t5、t2组成三相脉宽调制逆变器,c力图维持逆变器的输入直流电压ud为恒值, 因此,这一线路称为电压型逆变器。
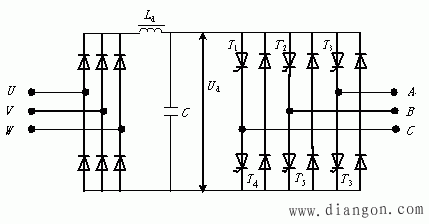
图2 (a) 电压型功率晶体管(gtr)三相逆变器主回路原理图


图2 (b) 电压型功率晶体管三相逆变器主回路波形图
逆变器开关元件t1、t2,t3的控制是由三角波1和按调速控制要求生成的具有一定频率和电压幅值的正弦波2,通过波形1和2的比较生成等幅、等距而不等宽的矩形脉冲3,作为控制其通断的控制信号的。从而在逆变器的输出端获得三组与控制波形3相似的矩形脉冲,这种波形在驱动电机时,其作用等效于三相正弦电压4。
由上面的讨论可知,实现变频调压的关键是逆变器控制端获得要求的控制波形3。控制波形的实现方式(即电机调速的控制方式),现在广泛采用的方式是矢量变换控制。
图3是交流伺服调速系统原理图的实例,该系统由功率变换器和控制平台两部分组成。功率变换器又由整流器和逆变器两部分构成,整流器的作用是将输入的三相交流电变换成直流电,如图3左上部所示;逆变器是将直流电按控制信号的要求变换成所需要的三相交流电,现在高性能逆变器常常采用新型的开关频率较高的ipm功率模块,如图3右上部所示。

图3 交流伺服调速系统实例
控制器平台的硬件上采用dsp+fpga的方案,如图3的下半部分所示。其中fpga(现场可编程门阵列)器件和dsp(数字信号处理器)的主要功能是与软件一起,实现对所有控制任务的调度,输入输出信号的处理、逆变器控制信号的生成以及其他控制功能等。at89c52实现对显示数码管、键盘(用于调试和参数设置)以及串口的管理。限于篇幅,各模块的详细作用,这里不再详细讨论了。
定位精度是的重要精度指标,该指标的提高与整个进给伺服系统的系统参数的合理选择有着密切的关系。通常定位精度使用定位误差来衡量的,即用期望的指令位置与实际位置之差进行评定,即有:
ec=xc-xo
在实际中定位精度的检测是在空载的情况进行的,即无负载力(fc =0),只有摩擦力。这样在检测过程中作为干扰输入的摩擦力和检测指令的位置输入都可以看成是系统的阶跃激励,即:

![]() 闭环系统的定位误差
闭环系统的定位误差


![]() 半闭环系统的定位误差
半闭环系统的定位误差

式中kr=ra/kt,kt是的转矩系数;k是机械执行部件的传动刚度系数。
![]() 讨论
讨论
由![]() 可知,为减小定位误差可采用下列措施:
可知,为减小定位误差可采用下列措施:
![]() 减小传动间的摩擦力fcr,如采用滚动传动取代滑动。
减小传动间的摩擦力fcr,如采用滚动传动取代滑动。
![]() 增大kn、ka,其实质增大ks(在系统稳定的范围内)。
增大kn、ka,其实质增大ks(在系统稳定的范围内)。
![]() 减小kr(=ra /kt),即选择kt较大的伺服电机。
减小kr(=ra /kt),即选择kt较大的伺服电机。
![]() 在半闭环系统中,要尽可能增大传动机构的刚度k,这是因为当k较小时,将产生较大的弹
在半闭环系统中,要尽可能增大传动机构的刚度k,这是因为当k较小时,将产生较大的弹
性变形,从而使定位误差增大。
1.系统增益的概念和意义
系统增益ks又称速度增益、开环增益,它是进给伺服系统的重要性能参数,其定义是单位位置误差△d所能控制的速度f,其量纲是1/sec:
ks=f/△d(1/sec) (1)
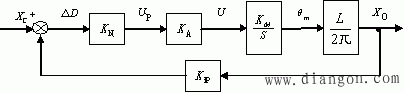
图1 传递函数简化框图
图1中:kn方框是位置控制单元的传递函数,kn是位置环增益(对比例调节而言);ka方框是速度控制单元的传递函数,ka是速度环增益;km/s方框是的传递函数,km是电机的增益系数;l/2π方框是机械执行单元的传递函数,l是传动丝杆的螺距;kfp方框是位置控制单元的传递函数,kn是位置检测比例系数;则此时进给伺服系统的传递函数为:

2.ks对系统动态性能(速度、加速度)的影响
![]() 系统的位置输入与位置输出的关系
系统的位置输入与位置输出的关系
在进给过程中位置输入可以看成是系统的斜坡激励:


![]() 讨论
讨论
![]() 系统增益ks越大,则时间常数越小,达到指令速度的时间越短,即系统响应快或系统灵敏度高。
系统增益ks越大,则时间常数越小,达到指令速度的时间越短,即系统响应快或系统灵敏度高。
![]() 系统的加速度与系统增益ks成正比例,即系统增益大,则加速度大。系统在刚启动的一瞬间,即时的加速度为
系统的加速度与系统增益ks成正比例,即系统增益大,则加速度大。系统在刚启动的一瞬间,即时的加速度为
![]()
可见当然启动时,ks越大可使系统的响应加快,但对系统的冲击也大,尤其对惯性较大的系统,将产生很大的冲击力,另外,加速度太大也可能系统超调,引起系统失稳。因此,系统增 益ks不能太大。
3.ks与跟随误差△d的关系
系统的跟随误差为:
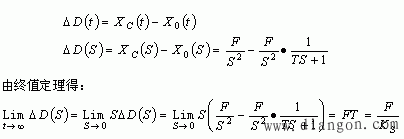
可知速度一定时,系统增益ks越大,则系统的稳态位置误差越小,即系统的随动误差小或者说跟随精度高。
,对系统的灵敏度、系统增益ks和系统的加速度这三个因素,在确定它们的数值时要进行折衷考虑。这样才能使系统获得较好的动态性能。
4.数控系统中ks的选取和设定方法
![]() ks的初选方法
ks的初选方法
在工程调试中,ks可按下列方式初选:

mm、ml:分别是电机的输出转矩和负载转矩;gdm、gdl:分别是电机转子和负载等效飞轮惯量。
![]() ks的设定方法
ks的设定方法
由前面的推导可知:
![]()
其中:ka、km、l/2π在数控系统、伺服系统和机械系统选定后便确定了,而kn是作为可调参数,允许用户根据具体情况选定,以满足系统的稳定性和快速度性的要求。通常在数控系统或伺服驱动单元中可对kn进行设定。
- 西门子CPU模块 1215C AC/DC14输入/10输出6ES7215-1BG40-0XB0
- 西门子S7-1200CPU1214C AC/DC4输入/10输出6ES7214-1BG40-0XB0
- 西门子6ES7214-1BG40-OXBO 上海西门子代理价格
- 西门子6ES7 214-1BG40-0XB0 西门子总代理 -源头供应
- 西门子6ES7214-1BG40-0XB0 官方授权代理商 PLC
- 6ES7215-1BG40-0XB0西门子模块
- SIEMENS西门子 继电器 6ES7 215-1BG40-0XB0
- 西门子6ES7215-1BG40-0XB0/CPU 1215C plc模块代理商
- 澳门西门子电源代理商6ES7214-1BG40-0XB0
- 香港西门子电源代理商6ES7214-1BG40-0XB0

